Everyone who knows how to make the Pascal’s triangle would be familiar with the obvious simple rule that governs its structure: the number below is the sum of the two numbers above it. Thus, we have the top numbers as: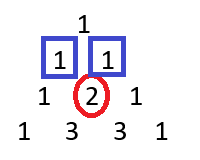 
So, I figured that if I use this simple rule, I might be able to extend the Pascal’s triangle upwards, like for example finding the two numbers on top of the apex number, which is 1.
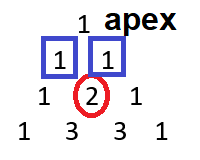
So, when I looked at the apex number, I had a problem of whether to use 0 + 1 = 1 or 1 + 0 =1. Ultimately, I used the former (although, you can use either because using the latter (i.e. 1 + 0) will generate a mirror extended Pascal’s triangle to what I’m going to show you):
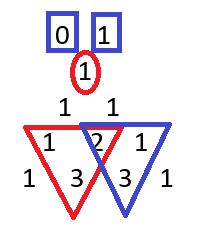
Next, I reverse-engineered both the 0 and 1 on top of the apex. I started with the latter with this:
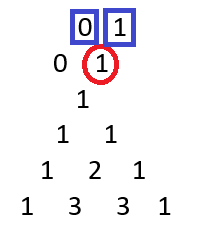
Then, I continued with this:
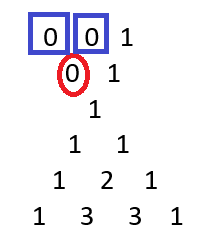
Following all the above rules, I came up with this extended Pascal’s triangle below on top of the original Pascal’s triangle (the ones in the yellow-colored boxes):
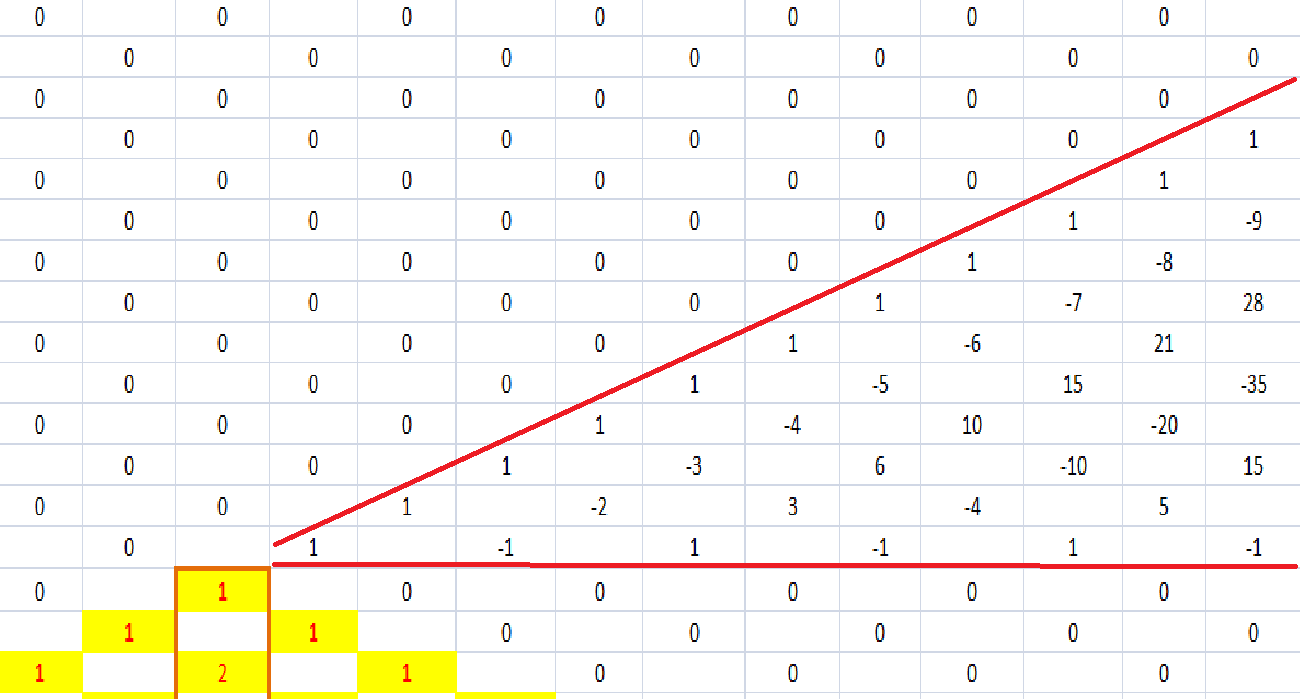
Did you find the Grandi’s series and the 1 − 2 + 3 − 4 + ··· infinite series in my extended Pascal’s triangle yet? Well, here’s the Grandi’s series:
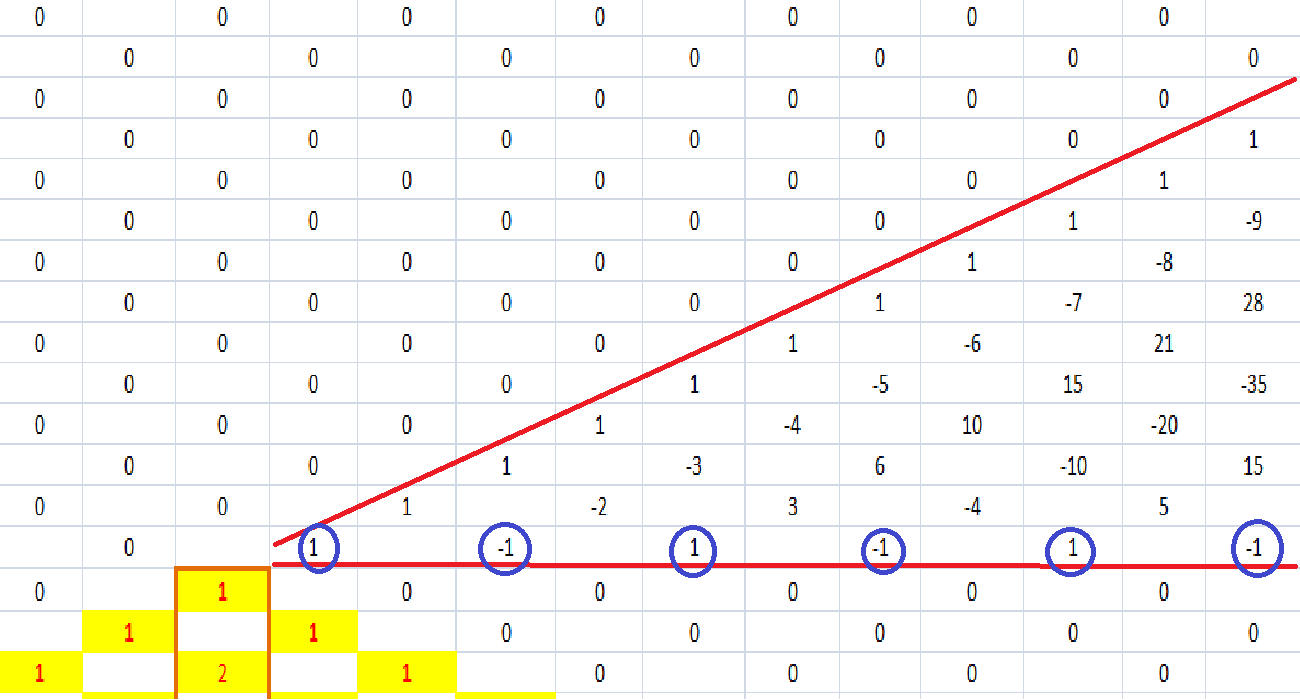
And here’s the 1 − 2 + 3 − 4 + ··· infinite series below:
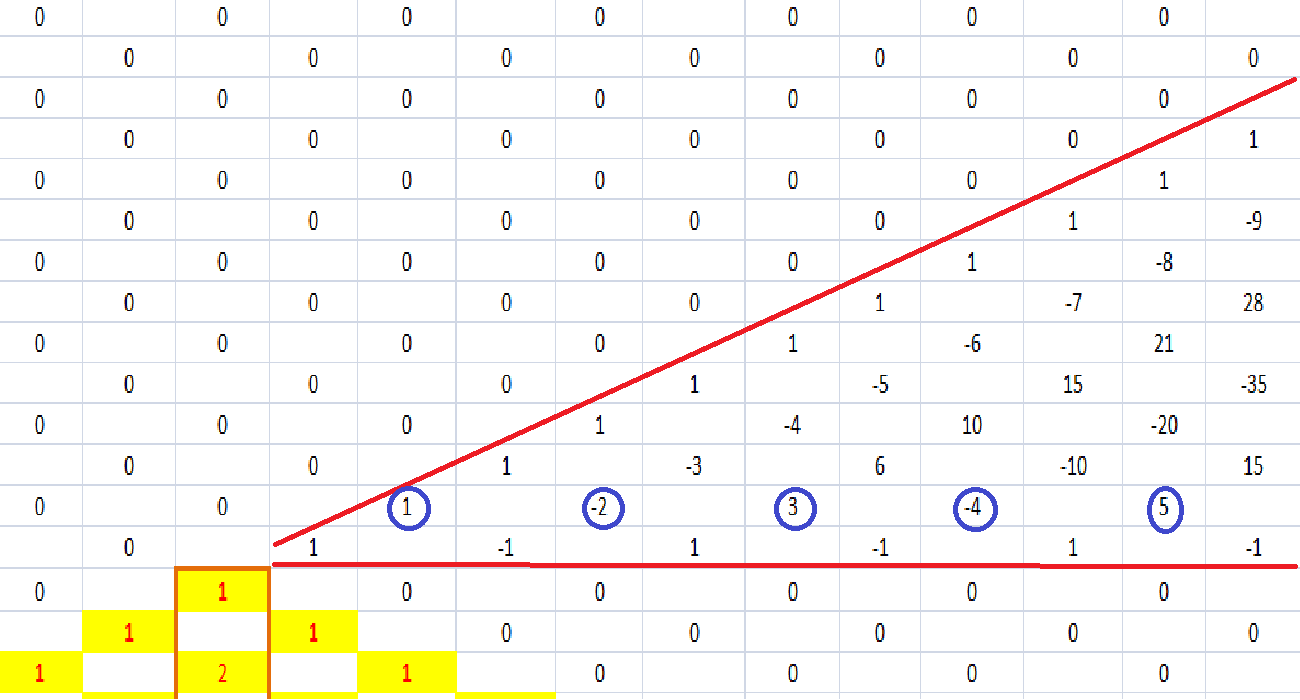
I also noticed that each of the numbers in the Grandi’s series are aligned with the prime numbers in the original Pascal’s triangle :
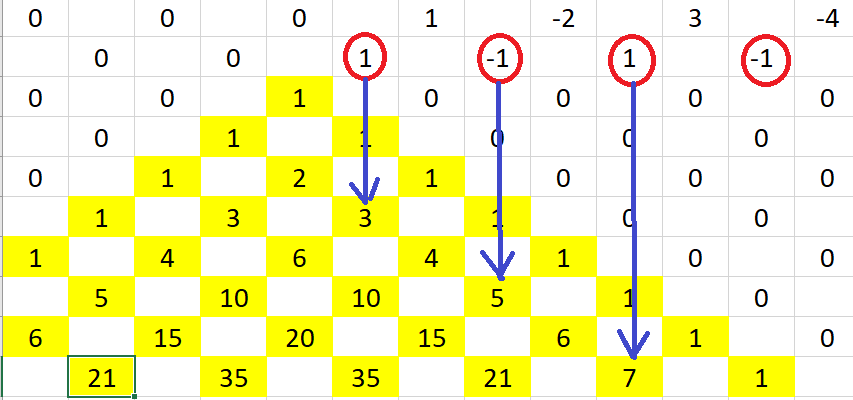And, as you might have already guessed, the 1 − 2 + 3 − 4 + ··· infinite series is also aligned with the original Pascal’s triangle’s composite numbers:
bernardbeduya 